Research

Menu:
Soft Sensors
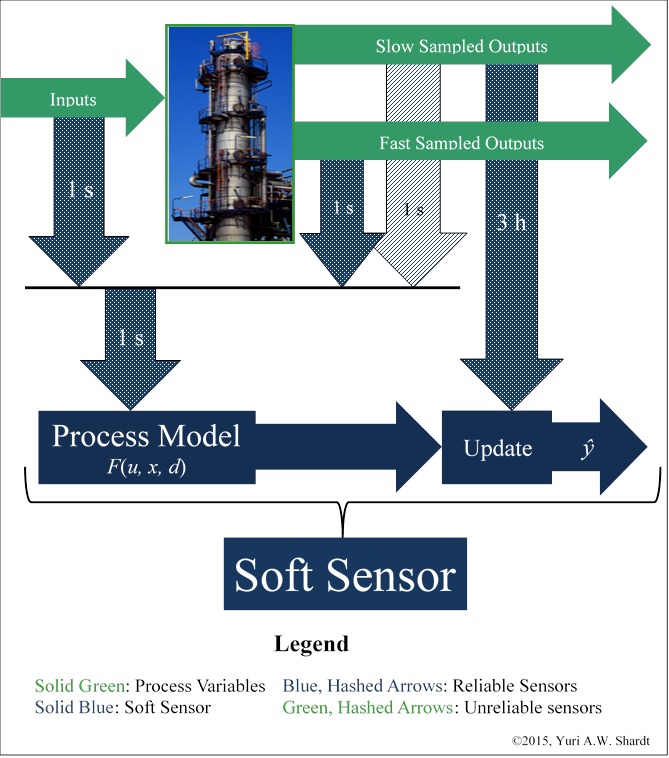
Soft, or inferential, sensors are a framework for dealing with imperfections in the measurement systems of complex processes [1, 2]. They can be applied to solve many different problems in industrial systems, including dealing with missing and faulty data and reconciling data from multiple different measurement devices. As well, soft sensors can overcome issues arising from the lack of data at the required frequency. Soft sensors find applications in a find range of different fields, including oil and gas [3, 4], chemical [5, 6, 7], and economic or key performance index-based analysis [8]. Figure 1 shows a block diagram representation of a soft sensor and its incorporation of different process information.
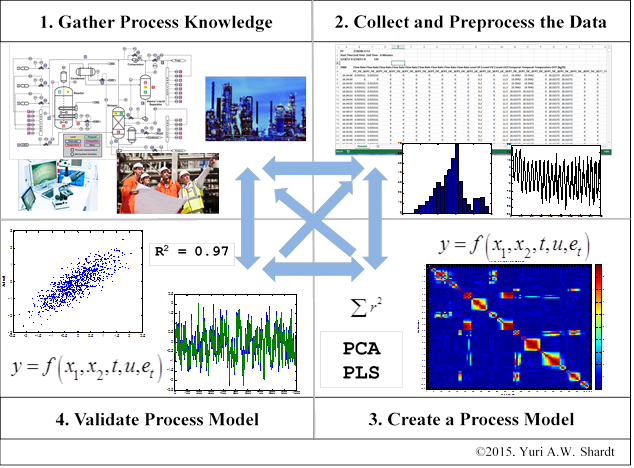
The design and implementation of a soft sensor can be split into 4 key tasks, which are shown schematically in Figure 2 [9, 3, 10]:
- Gather process knowledge and understanding: In this step, a thorough understanding of the process and design objectives is obtained by consulting the relevant people, including plant operators and managers.
- Data collection and preprocessing: In this step the data is analysed to determine the quality and usefulness of it for soft sensor design. Issues such as missing or faulty data, outliers, and incomplete process knowledge will often require a return to step 1) in order to obtain additional information.
- Process Modelling: In this step, a model of the process is obtained using any available methods, ranging from simple regression analysis to complex, data-driven methods. The goal is to develop a model that can not only accurately predict future process values, but be robust enough to deal with variations in plant operations. Methods used included modifications of linear regression [11], principal component analysis [5], support vector regression [6], and online updating methods [7]. When dealing with missing or faulty data, methods such as the expectation-maximisation algorithm [12, 13], Bayesian methods [12], or various forms of the Kalman filter have been used [14, 15].
- Model Validation: Once a model has been thoroughly tested off site, it needs to be validated online, in real time, at the industrial site. Doing this can reveal new problems, such as issues with the input data or unexpected performance behaviour, that need to be dealt with. At this point, different bias update terms can be tested in order to determine the best one. Furthermore, porting the model from the computer-based solution to a solution that will allow for efficient and effective online, industrial implementation can require much effort. Often the model will need to be simplified or redesigned due to computational demands.
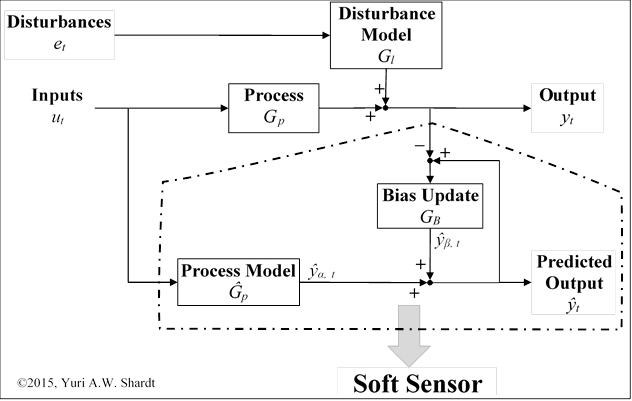
Mathematically, a soft sensor system can be described as shown in Figure 3 [17]. This mathematical description consists of two parts: the model and the bias update term. Partitioning the system into two components allows for a better understanding and modelling of the process. In short, this approach implies that the model is good at capturing the trends in the process, but may have issues with obtaining the correct absolute value. This issue can be compensated by using an appropriately designed bias update term. Furthermore, the bias update term can deal with such issues as time delay in obtaining the desired process values and a slower, different sampling rate.
The key challenges in soft sensor design lie in the development of robust, efficient, and fast methods for modelling complex, highly interacting systems and the development of appropriate techniques for delaying with time delay and sampling rates in cases where such are not well characterised. Finally, application of soft sensors to such areas of fault detection, as well as new industries, such as the hot mill steal industry, still requires a lot of work in order to deal with the demands for accuracy and given performance.
References
- Yuri A.W. Shardt (2012). Data Quality Assessment for Closed-Loop System Identification and Forecasting with Application to Soft Sensors, Doctoral Thesis, University of Alberta. Online access.
- Luigi Fortuna, Salvatore Graziani, Alessandro Rizzo, and Maria G. Xibilia (2007). Soft Sensors for Monitoring and Control of Industrial Processes, London, United Kingdom: Springer-Verlag.
- Shima Khatibisepehr, Biao Huang, and Swanand Khare (2013). “Design of inferential sensors in the process industry: A review of Bayesian methods,” Journal of Process Control, 23 (10), pp. 1575-1596.
- Elom Domlan, Biao Huang, Fangwei Xu, and Aris Espejo (2011). “A decoupled multiple model approach for soft sensor design,” Control Engineering Practice, 19, pp. 126–134.
- Eliana Zamprogna, Massimiliano Barolo, and Dale E. Seborg (2005). “Optimal selection of soft sensor inputs for batch distillation columns using principal component analysis,” Journal of Process Control, 15 (1), pp. 39-52.
- Kiran Desai, Yogesh Badhe, Sanjeev S. Tambe and Bhaskar D. Kulkarni (2006). “Soft-sensor development for fed-batch bioreactors using support vector regression,” Biochemical Engineering Journal, 27 (3), pp. 225-239.
- Koichi Fujiwara, Manabu Kano, Sinji Hasebe, and Akitoshi Takinami (2009). “Soft-sensor development using correlation-based just-in-time modeling,” AIChE Journal, 55 (7), pp. 1754-1765.
- Yuri A.W. Shardt, Haiyang Hao, and Steven X. Ding (2014). “A New Soft-Sensor-Based Process Monitoring Scheme Incorporating Infrequent KPI Measurements” in IEEE Transactions on Industrial Electronics, 62 (4), pp. 3843-3851. doi:10.1109/TIE.2014.2364561.
- Shima Khatibisepehr, Biao Huang, Swanand Khare, Elom Domlan, Fangwei Xu, Aris Espejo, and Ramesh Kadali (2014). “A probabilistic framework for real-time performance assessment of inferential sensors,” Control Engineering Practice, 26, pp. 136-150.
- Bao Lin, Bodil Recke, Jørgen K. H. Knudsen, and Sten Bay Jørgensen (2007). “A systematic approach for soft sensor development,” Computers and Chemical Engineering, 31, pp. 419-425.
- Jialin Liu, Ding-Sou Chen and Jui-Fu Shen (201). “Development of Self-Validating Soft Sensors Using Fast Moving Windows Least Squares,” Industrial & Engineering Chemistry Research, 49, pp. 11530-11546.
- Shima Khatibisepehr and Biao Huang (2008). “Dealing with Irregular Data in Soft Sensors: Bayesian Method and Comparative Study,” Industrial & Engineering Chemistry Research, 47 (22), pp. 8713-8723.
- Xing Jin, Siyun Wang, Biao Huang, and Fraser Forbes (2012). “Multiple model based LPV soft sensor development with irregular/missing process output measurement,” Control Engineering Practice, 20 (2), pp. 165-172.
- Ming T. Tham, Gary A. Montague, A. Julian Morris, and Paul A. Lant (1991). “Soft-sensors for process estimation and inferential control,” Journal of Process Control, 1 (1), pp. 3-14.
- Petr Kadlec, Bogdan Gabrys, and Sibylle Strandt (2009). “Data-driven Soft Sensors in the process industry,” Computers & Chemical Engineering, 33 (4), pp. 795-814.
- Shen Yin, Hao Luo, and Steven X. Ding (2014). “Real-Time Implementation of Fault-Tolerant Control Systems With Performance Optimization,” IEEE Transactions on Industrial Electronics, 61 (5), pp. 2402-2401.
- Yuri A.W. Shardt and Biao Huang (2012). “Tuning a Soft Sensor’s Bias Update Term. 1. The Open-Loop Case” in Industrial and Engineering Chemistry Research, 51 (2), pp. 4958-4967. doi:10.1021/ie201456z.
- Yuri A.W. Shardt and Biao Huang (2012). “Tuning a Soft Sensor’s Bias Update Term. 2. The Closed-Loop Case” in Industrial and Engineering Chemistry Research, 51 (2), pp. 4968-4981. doi:10.1021/ie2014586.